Contoh Soal Logika Matematika dan Pembahasannya SMA Kelas 10
Contoh Soal Logika Matematika - Pada kelas 10, siswa dan siswi SMA memperoleh materi pelajaran matematika yang bernama logika matematika. Pada bab tersebut para murid akan diajarkan untuk menggunakan logika pemikiran mereka guna menyelesaikan persoalan yang berhubungan dengan pernyataan-pernyataan. Dari pernyataan-pernyataan yang diberikan mereka diharuskan untuk menarik berbagai jenis kesimpulan mulai dari negasi, konjungsi, disjungsi, implikasi, biimplikasi dan berbagai operasi lainnya.
Rumus matematika dasar sengaja memberikan beberapa contoh soal pada artikel ini guna membantu kalian dalam memahami konsep logika matematika dan mengerti bagaimana langkah-langkah yang harus diambil untuk menjawab soal-soal yang berkaitan dengan materi tersebut. Ini dia contoh soal yang dapat kalian gunakan untuk berlatih dan memperdalam pengetahuan tentang materi logika matematika yang diajarkan oleh guru kalian di sekolah.
Contoh Soal Latihan Logika Matematika dan Pembahasan Lengkap
Soal 1
Coba kalian tentukan negasi dari beberapa pertanyaan di bawah ini:
A. Kemarin Bandar Lampung hujan.
B. Amir anak pintar.
C. Kura-kura memiliki sayap.
D. Guru SMA Taruna Jaya memakai batik pada hari Kamis.
Pembahasan:
Negasi adalah ingkaran atau dari sebuah pernyataan atau hal yang bertolak belakang dengan pernyataan tersebut, maka:
A. Tidak benar bahwa kemarin Bandar Lampung hujan.
B. Tidak benar bahwa Amir anak pandai.
C. Tidak benar bahwa kura-kura memiliki sayap.
D. Tidak benar bahwa guru SMA Taruna Jaya memakai batik pada hari Kamis.
Atau bisa juga diubah menjadi:
A. Kemarin Bandar Lampung tidak hujan.
B. Amir bukan anak pintar.
C. Kura-kura tidak memiliki sayap.
D. Guru SMA Taruna Jaya tidak memakai batik pada hari Kamis.
Soal 2
Tentukanlah negasi dari pernyataan-pernyataan di bawah ini:
A. p = Semua karyawan memakai seragam biru pada hari Jum'at.
B. p = Semua murid mengikuti ujian nasional hari ini.
C. p = Semua jenis ikan bernafas dengan insang.
Pembahasan:
Di dalam negasi, kata-kata "semua/setiap" diganti dengan kata "beberapa/ada" maka jawaban dari soal di atas adalah:
A. ~p = Ada karyawan yang tidak memakai seragam biru pada hari Jum'at.
B. ~p = Beberapa murid tidak mengikuti ujian nasional hari ini.
C. ~p = Beberapa jenis ikan tidak bernafas dengan insang.
Soal 3
Coba kalian ubah pasangan-pasangan pernyataan di bawah ini menjadi pernyataan majemuk dengan operasi majemuk (dan):
A. p: Hari ini surabaya cerah
q: Hari ini surabaya udaranya sejuk
B. p: Gilang mengenakan baju merah
q: Gilang mengenakan topi hitam
C. p: Bejo pandai dalam pelajaran matematika
q: Bejo pandai dalam pelajaran kimia
Pembahasan:
Pada operasi konjungsi, pernyataan positif dapat digabungkan dengan kata "dan" serta menghilangkan kata-kata yang sama, maka:
A. p^q : Hari ini surabaya cerah dan udaranya sejuk.
B. p^q : Gilang mengenakan baju merah dan topi hitam
C. p^q : Bejo pandai dalam pelajaran matematika dan kimia
Jika pernyataannya bertolak belakang, kita bisa mengganti kata "dan" dengan kata "meskipun" ataupun "tetapi".
Soal 4
Amati pernyataan berikut ini:
p : Hari ini ahmad pergi ke toko buku
q : Hari ini ahmad pergi ke supermarket
Ubah kedua pernyataan diatas dengan logika matematika di bawah ini:
A. P^q
B. P^~q
C. ~p^q
D. ~p^~q
Pembahasan:
A. Hari ini Ahmad pergi ke toko buku dan supermarket
B. Hari ini Ahmad pergi ke toko buku dan tidak ke supermarket
C. Hari ini Ahmad tidak pergi ke toko buku tetapi ke supermarket
D. Hari ini Ahmad tidak pergi ke toko buku dan tidak ke supermarket
Soal 5
Gabungkanlah beberapa pernyataan di bawah ini dengan operasi disjungsi (atau):
A. P: Rani pergi ke pasar
q: Rani menanak nasi
B. p: Dani mengajar Bahasa Indonesia
q: Dani mengajar Matematika
Pembahasan:
A. pvq = Rani pergi ke pasar atau menanak nasi
B. pvq = Dani mengajar bahasa indonesia atau matematika
Soal 6
Tentukan konvers, invers dan kontraposisi dari pernyataan di bawah ini:
"Jika hari ini hujan maka Wayan mengendarai mobil"
Pembahasan:
Pernyataan di atas adalah implikasi p -> q sehingga:
p: Hari ini hujan
q: Wayan mengendarai mobil
Konvers dari pernyataan tersebut adalah q -> p
"Jika Wayan mengendarai mobil maka hari ini hujan"
Invers dari pernyataan di atas adalah ~p -> ~q
"Jika hari ini tidak hujan maka Wayan tidak mengendarai mobil"
Kontraposisi dari pernyataan tersebut adalah ~q -> ~p
"Jika Wayan tidak mengendarai mobil maka hari ini tidak hujan"
Soal 7
Tentukan kesimpilan dari premis berikut:
Premis 1 : Jika Panji rajin belajar maka ia lulus ujian
Premis 2 : Jika Panji lulus ujian maka ia masuk universitas
Pembahasan:
Kita gunakan prinsip silogisme
p -> q
q -> r
________
∴ p → r
Maka kesimpulannya adalah : "Juka Panji rajin belajar maka ia masuk universitas"
Soal 8
Tentukanlah kesimpulan dari dua buah premis berikut:
premis 1 : Jika harga BBM turun maka harga cabai turun
premis 2 : Harga cabai tidak turun
Pembahasan:
p: Harga BBM turun
q: Harga cabai turun
kita simpulkan dengan menggunakan modus Tollens
p → q
~q
_______
∴ ~p
Maka kesimpulan dari premis di atas adalah "Harga BBM tidak turun"
Itulah beragam Contoh Soal Logika Matematika dan Pembahasannya untuk kalian yang duduk di bangku SMA Kelas 10. Harapannya adalah agar kalian semakin memahami konsep-konsep logika matematika sehingga nantinya mampu menyelesaikan persoalan-persoalan matematika mengenai logika matematika dengan baik dan benar.
Latihan Soal
Kumpulan Soal Logika Matematika
- Jika sobat diberikan pernyataan ( p ∨ ~q), maka konvers dari penyataan tersebut adalah
a. p → (~p ∨q) c. p → (p∨~q) e. p → (~p∧~q) b. p → (p ∧~q) d. p → (~p∨~q) - Jika p bernilai salah, q benar, sedangkan ~p dan ~ q merupakan ingkaran dari p dan q, maka pernyataan di bawah ini yang benar adalah:
a. ~p ⇒ ~q bernilai benar c. p ⇒q bernilai salah e. p ⇒q bernilai benar b. ~q ⇒ ~p bernilai salah d. ~p ⇒q bernilai salah - Pernyataan (p∨q) ⇒ bernilai salah jika
a. p benar dan q benar c. p salah q benar e. bukan semuanya b. p benar q salah d. p salah q salah - Jika ada sebuah pernyataan majemuk : Jika hari hujan maka jalan-jalan di jakarta akan banjir ekivalen dengan pernyataan
a. Hari hujan dan jalan-jalan di Jakarta Banjir b. Jika jalan-jalan di Jakarta banjir maka hari hujan c. Hari tidak hujan dan jalan-jalan di Jakarta tidak banjir. d. Jika hari tidak hujan maka jalan-jalan di jakarta tidak banjir - Ingkaran dari pernyataan “Semua peserta tes bedoa sebelum mengerjakan soal”
a. Semua peserta tes tidak berdoa sebelum mengerjakan tugas b. Beberapa peserta tes berdoa sebelum mengerjakan soal c. Beberapa peserta tes tidak beroa sebelum mengerjakan soal d. Beberapa peserta tes berdoa setelah mengerjakan soal - Pernytaan : “Jika hari gelap maka lampu dinyalakan” ekivalen dengan pernyataan
a. Jika lampu tidak dinyalakan maka hari tidak gelap b. Jika hari gelap maka lampu tidak dinyalakan c. Jika tidak gelap maka lampu tidak dinyalakan d. Jika hari tidak gelap maka lampu dinyalakan - Jika sobat diberika pernyataan “Jika semua siswa menyukai matematika maka guru senang mengajar“. Konta posisi dari pernyataan tersebut adalah …
a. Jika guru senang mengajar pasti ada siswa yang tidak suka matematika b. Jika tidak semua siswa suka matematika maka guru tidak senang mengajar c. Jika guru tidak senang mengajar maka ada siswa yang suka matematika d. Jika guru tidak senang mengajar maka ada siswa yang tidak suka matematika - Ingkaran dari pernyataan √15 < 4 jika dan hanya jika sin 30o < sin 45o adalah
a. √15 <= 4 jika dan hanya jika sin 30o < sin 45o b. √15 < 4 jika dan hanya jika sin 30o > sin 45o c. √15 >= 4 jika dan hanya jika sin 30o > sin 45o d. √15 < 4 jika dan hanya jika sin 30o >= sin 45o e. √15 < 4 jika dan hanya jika sin 30o = sin 45o - Kontraposisi dan implikasi dari penyataan “Jika saya lulus ujian saya akan puasa nazar”
a. Jika saya puasa nazar maka saya lulus ujian b. Jika saya lulus ujian, saya tidak akan puasa nazar c. Jika saya tidak lulus ujian maka saya tidak puasa nazar d. Jika saya tidak puasa nazar maka saya tidak lulus ujian - Ingkaran dari pernyataan (p ∧ q) → q
a. (p∧q) ∧ ~q c. ~(p∧q) ∧ q e. (p∧q) ∨ ~q b. (p∧q) ∧ q d. (~p∨~q) ∨ ~q - “Jika binatang itu kuda, maka binantang itu berkaki empat”Ternyata binatang itu tidak berkaki empatKesimpulannya adalah …
a. binatang itu kuda b. binatang itu bebek c. binatang itu pasti bukan ayam d. binatang itu bukan kuda d. pasti itu kudanil - Sobat hitung diberika pernyataan “Hanya jika sobat bekerja keras, sobat akan sukses”jika ternyata sobat selalu bekerja keras, maka pernyataan berikut yang benar adalah …
a. Sobat selalu sukses b. Sobat tidak pernah sukses c. Kamu kadang-kadang sukses d. Tidak ada yang dapat disimpulkan e. Bukan semuanya - Diketahui argumentasi
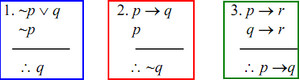diantara argumentasi logika matematika di atas manakah yang sah adalaha. 1,2,4 saja c. 1 dan 3 e. 3 saja b. 1 dan 2 d. 2 saja - Pernyataan “Jika dia merah, maka dia adalah darah”Pernyataan berikut yang benar adalah …I. Dia tidak merah, maka dia bukan darahII. Dia adalah darah, maka dia adalah merahIII. Dia bukan darah, maka dia tidak merah
a. hanya I c. hanya III e. II dan III b. hanya II d. I dan III - Pernyataan : “Jika laba tinggi maka karyawan sejahtera” mempunyai invers yaitu
a. Jika laba tinggi maka karyawan tidak sejahtera b. Jika laba rendah maka karyawan tidak sejahtera c. Jika laba rendah maka karyawan sejahtera d. Jika laba tinggi maka karyawan sejahtera e. Jika laba tinggi maka karyawan tidak sejahtera - Kontraposisi pernyataan “Jika saya mengantuk saya akan tidur” adalah
a. Jika tidak mengantuk, saya tidak tidur b. Saya mengantuk, saya nonton liga inggris c. Saya tidak mengantuk dan saya tidak tidur d. Saya tidak tidur, saya bermain ping pong e. Jika saya tidak tidur maka saya tidak mengantuk - Ingkaran dari pernyataan “Jika sobat rajin belajar maka sobat tidak lulus USM STAN” adalah
a. Sobat rajin belajar dan sobat tidak lulus USM STAN b. Sobat rajin belajar dan sobat lulus USM STAN c. Sobat rajin belajar atau sobat lulusUSM STAN d. Sobat tidak rajin belajar dan sobat tidak lulus USM STAN - a, b, c, dan d adalah pernyataan. Jika pernyataan-pernyataan berikut bernilai benarp ∧ qp ⇔ rr ⇔ s
a. p∨q c. p ⇒q b. ~ p∨q d. -p⇒-s - Ada 2 pernyataan:I. Beberapa bilangan bukan bilangan primaII. Tidak ada bilangan prima yang merupakan bilangan kuadratJika beberapa berarti “Paling sedikit sat”, maka dari pernyataan I dan II dapat disimpulkan
a. Beberapa bilangan dalah bilangan kuadrat b. Beberapa bilangan kuadrat bukan bilangan c. Beberapa bilangan bukan bilangan kuadrat d. Tidak ada bilangan yang bilangan kuadrat e. Tidak satupun yang di atas merupakan kesimpulan pernyataan I dan II - Perhatikan ungkapan: “Semua pemain tinju berbadan kekar.” Negasi ungkapan tersebut adalah
a. Tidak ada pemain tinju yang erbadan kekar b. Beberapa pemain tinju berbadan kekar c. Beberapa pemain tinju berbadan biasa d. Semua pemain tinju berbadan biasaa d. Tidak ada pemain tinju yang berbadan biasa. - Pernyataan “Jika Ririn lulus ujian, maka ririn akan langsung akad nikah” senilai dengan …
a. Jika ririn lulus, maka ririn akan akad nikah b. Jika ririn tidak lulus ujian, maka ririn akan akad nikah c. Jika ririn tidak lulus ujian, maka ririn tidak akad nikah d. Jika ririn tidak akad nikah, maka ririn tidak lulus ujian
~~~~SelamatMengerjakan~~~~
Sumber :
Tidak ada komentar:
Posting Komentar